Number as relations

Ivor collects pencils. Ivor’s mum gave him 7 pencils. His dad gave him 4 more. Ivor gave 6 of his pencils to his sister. Did Ivor end up with more or fewer pencils than he started with? How many?
Both of these ‘problems’ (yes, problems is in scare quotes because they are the type you only meet in school maths, but bear with me, they have a purpose) can be answered by calculating 7 + 4 − 6 (and yes, there are other ways).
Yet children find the second problem much harder than the first. In fact, since we are not told how many stickers Ivor started off with, some children will say that the second problem cannot be answered. Why do they find it more difficult?
The difficulty is in the nature of the answers. In the first problem, five represents a quantity - the number of stickers Ivor ends up with. But the answer five to the second problem represents a relationship - how many more stickers Ivor had than when he started.
We often switch between using numbers as quantities and numbers as relations without paying attention to the distinction. But awareness of the distinction is important in supporting children’s developing number sense.
Take a simple calculation like:
7 − 3 = 4
If we read the ‘−’ as ‘take away’ then the answer four is a quantity - it is the quantity remaining when three things (stickers, marbles, zingbats) are removed from seven. When we ‘take away’ we can hold up the particular quantity that is left behind.
Reading ‘−’ as ‘difference between’, the four then represents a relationship - how many more there are in a collection of seven objects then there are in a collection of three. Unlike ‘taking away’, when comparing two collections there is no particular quantity from the larger collection that specifically makes up the difference. Four expresses an abstract relationship between seven and three.
I often invite teachers to show what picture they might draw to help a child understand 7 − 3. Almost invariably people draw seven objects and strike out, or somehow bracket off, three of them.
It is very rare for someone to draw a set of seven and another set of three and point up the difference. Even adults seem to prefer the concrete, the quantity, over the abstract, the relationship.
To fully develop children’s number sense we need to make sure that they get a rich diet of operating with numbers as relationships as well as quantities. I’ll be exploring this in future blogs.
Meanwhile, if you would like to read more about the research behind this, there is a great, free, set of reports - Key Understandings in Mathematics Learning - that you can download from the Nuffield Foundation website.
No hands up please

Chatting after the lesson, the teacher was bemused over Tony’s willingness, as he wasn’t that mathematically confident.
Having watched the lesson unfold it was clear that the teacher did what many teachers do: wait for several children to put their hands up before selecting someone to answer. I think Tony had figured out that the easiest way NOT to get picked was to be the first person to volunteer the answer.
The routine of ‘hands up’ is so ubiquitous in maths lessons that it can seem as natural as the sky looking blue, water feeling wet and Cliff Richard staying young.
But just because ‘it’s always been that way’ isn’t a good reason to carry on with some classroom practices. And there is good evidence that ‘hands up’ may not be the best practice.
How do you know if you are good at maths?
Dropping into a maths class I will often ask the children this question. There is a remarkable degree of agreement in the answers, which are usually along the lines of:
You’re good at maths if you can do it quickly and easily.
The practice of ‘hands-up’ for answers perpetuates the belief of speed as being the essence of being good at maths. Children who need a bit longer to figure things out simply don’t have the time they need or are discouraged when others around them get a hand up first.
The psychologist Carole Dweck has looked at the downside of such an attitude to learning and one of her perhaps surprising findings is that such beliefs hamper successful students as much as the less successful.
If you’ve been successful at school maths because you can do what is set without much effort, then what happens when the time comes (and it will) that you meet some maths that isn’t easily done and requires more effort? Dweck’s research shows that many learners then think along the lines of ‘perhaps I was wrong, I ‘m not that good at maths after all’ and conclude that maybe maths isn’t for them.
Behind this, Dweck argues, is whether learners view mathematical ability as a gift—something that you either have or not - or whether they view it as something that can be developed through practice and effort - a growth mindset.
The message is clear over-emphasis on quick answers perpetuates the ‘gift’ view of mathematical ability. ‘ Hands up’ leads to everyone losing out mathematically: the lower attainers in the short term, the higher attainers long-term.
A quiet ’thumbs up’ (held still against the chest) can still signal to the teacher when learners are ready, provide a calmer space within which to think, and dispel the myth that mathematical ability is all about speed.
blog comments powered by Disqus
Creativity and Primary Mathematics
ODD ONE OUT
23 20 15 25
Which number is the odd one out?
Most people’s immediate response to ‘Odd one out’ is that 20 is ‘odd’ because it is ‘even’ (pun intended!). A moment’s reflection can open up a seemingly closed problem like this to some creative thinking.
Can we find a reason for each of these numbers being singled out as the odd one?
And how many different reasons for each number?
Here are some starters for 25. It is the only number in the set that:
is a perfect square number
is a factor of 125
has an odd number of factors
has digits that add to seven
….
Thinking creatively can engage learners in mathematical reasoning with the different reasons given acting as springboards for further inquiry:
Can you find some other numbers with exactly three factors?
How many numbers under 100 have digits that add to 7?
Creativity as a key to deeper learning?
One popular argument for encouraging creativity is that we live in times of rapid change and being creative helps learners cope with such changes. Over and above this the work of the psychologist Ellen Langer suggests that creativity can have other payoffs.
Langer has extensively researched what she calls the conditionality of knowledge: that what we hold to be ‘true’ relies on certain conditions (in this case 20 is the odd one out under the conditions of odd and even numbers).
Langer’s research on Mindful Learning shows that treating knowledge as ‘conditional’ rather than ‘absolute’ not only leads to creativity but also to deeper learning of the knowledge being explored. In other words, justifying a range of answers may help kids become mathematically smarter.
I discuss these ideas more fully in my new book ‘Transforming Primary Mathematics’
Mindful mathematics
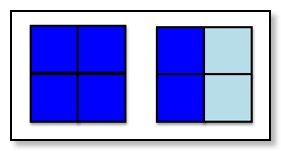
Ellen Langer
I was lucky this week to hear the wondrous Ellen Langer give a talk. If you haven’t come across it, then I highly recommend her book ‘The Power of Mindful learning’. She spoke for over two hours and it was pure enchantment.
One of the key findings from Prof Langer’s research of over 30 years is that learning is more powerful if we are mindful of the conditionality of most ‘facts’. For example, in a lesson on fractions, a diagram like the one above is usually introduced as the pale blue shows ½. In contrast, Langer argues that presenting the diagram as it ‘could’ represent ½ makes the learning mindful and deeper.
Part of the argument for this is that the ‘fractions’ are not in the diagram itself but they are the result of someone somewhere at sometime deciding how the diagram should be read. In other words, there was a choice to be made over what mathematics the diagram could represent - not what it does represent.
By re-introducing this choice and conditionality into the teaching of it, the learner is encouraged not simply to take the mathematics for granted, nor to just commit something to memory. In contrast they engage in mathematical thinking.
So what else could the pale blue represent?
Well, it could be different if we are mindful of not taking for granted the condition that the ‘unit’ has to be four small squares. Under the condition of the whole picture as the unit, then the pale blue could be ¼.
Or we could set up the condition of comparing the pale blue to the dark blue and so the pale blue could be ⅓. The possibilities do not end there.
Of course this does not mean telling children that ‘anything goes’ and they are free to choose any reading they like. But by implicitly acknowledging in our teaching the human agency in mathematics we could help more learners come to see mathematics as a human endeavour worth engaging with, rather than something to keep at arm’s length.
blog comments powered by Disqus
What's the point?
At the age of eleven, I began Euclid, with my brother as my tutor. This was one of the great events of my life, as dazzling as first love. I had not imagined there was anything so delicious in the world.
Bertrand Russell
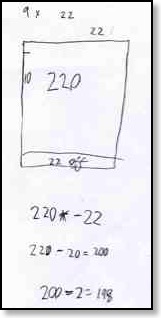
Running a teachers’ professional development session recently, I was sharing some children’s mathematics. The children had investigated constructing arrays that allowed them to calculate products in a variety of ways. For example, one child explored how nine times twenty-two could be modelled from an array for ten times twenty-two by slicing off a ‘strip’ to reduce one side to nine.
The array presents a powerful model of why what might become a rule of thumb (to multiply by nine, multiply by ten and subtract the original number) is grounded in mathematical structure.
I got the teachers exploring 75 x 89 in similar ways, for example starting with an array for 100 x 89 and then working with the array and using halving to get to 75 x 89.
Towards the end of the session I got the ‘what’s the point?’ question.
This question often hangs in the air but there is not always someone brave enough to voice it. I asked for elaboration and the teacher declared that such activity was meaningless and had nothing to do with ‘real-life’. Taking a risk I asked the group (of around 120) whether anyone had actually found the activity meaningful. Thankfully around 2/3 of the room put their hands up. The questioner persisted that the activity was meaningless, despite my pointing out that since that clearly was not the case for the majority of people in the room, the activity itself could not be regarded as meaningless, only some people’s response to it.
We talk about mathematical tasks as having ‘meaning’ or being ‘rich’ but course tasks do not have ‘meaning’ or ‘richness’; these are qualities that people engaged in the tasks bring to them.
The discussion with the teachers moved in the direction that schools are advised to always relate mathematics to ‘real-life’, coming back to the utilitarian argument for mathematics. I’m not convinced that ‘utility’ actually does succeed in making mathematics more meaningful for more children. For some, yes, but for many children playing around with ideas can be ‘meaningful’ in much the same way that people find meaning in playing the piano, painting an abstract, or reading poetry; activities each of which could equally be argued as having little immediate impact on people’s lives.
The idea that someone might engage with playing with mathematical ideas simply for the intrinsic pleasure of the play itself is alien to many. But that’s not the fault of with mathematics itself, and all to do with the way we continue to teach it.
