What's the point?
At the age of eleven, I began Euclid, with my brother as my tutor. This was one of the great events of my life, as dazzling as first love. I had not imagined there was anything so delicious in the world.
Bertrand Russell
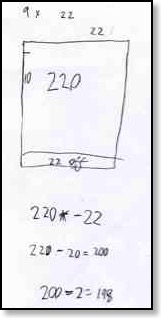
Running a teachers’ professional development session recently, I was sharing some children’s mathematics. The children had investigated constructing arrays that allowed them to calculate products in a variety of ways. For example, one child explored how nine times twenty-two could be modelled from an array for ten times twenty-two by slicing off a ‘strip’ to reduce one side to nine.
The array presents a powerful model of why what might become a rule of thumb (to multiply by nine, multiply by ten and subtract the original number) is grounded in mathematical structure.
I got the teachers exploring 75 x 89 in similar ways, for example starting with an array for 100 x 89 and then working with the array and using halving to get to 75 x 89.
Towards the end of the session I got the ‘what’s the point?’ question.
This question often hangs in the air but there is not always someone brave enough to voice it. I asked for elaboration and the teacher declared that such activity was meaningless and had nothing to do with ‘real-life’. Taking a risk I asked the group (of around 120) whether anyone had actually found the activity meaningful. Thankfully around 2/3 of the room put their hands up. The questioner persisted that the activity was meaningless, despite my pointing out that since that clearly was not the case for the majority of people in the room, the activity itself could not be regarded as meaningless, only some people’s response to it.
We talk about mathematical tasks as having ‘meaning’ or being ‘rich’ but course tasks do not have ‘meaning’ or ‘richness’; these are qualities that people engaged in the tasks bring to them.
The discussion with the teachers moved in the direction that schools are advised to always relate mathematics to ‘real-life’, coming back to the utilitarian argument for mathematics. I’m not convinced that ‘utility’ actually does succeed in making mathematics more meaningful for more children. For some, yes, but for many children playing around with ideas can be ‘meaningful’ in much the same way that people find meaning in playing the piano, painting an abstract, or reading poetry; activities each of which could equally be argued as having little immediate impact on people’s lives.
The idea that someone might engage with playing with mathematical ideas simply for the intrinsic pleasure of the play itself is alien to many. But that’s not the fault of with mathematics itself, and all to do with the way we continue to teach it.
Global education, global competition?

The Age
The novel and movie, Never Let Me Go, paints a chilling picture of children whose destinies are determined from birth. Without spoiling the plot for anyone not familiar with it, the story revolves around a group of children who are educated to accept their roles in a society that treats (some) humans as commodities, bred only for the service of others.
Never Let Me Go is set in a fictional parallel world, but the rhetoric from England, far from being science fiction, suggests schooling there is heading towards the grooming of children for particular destinations.Education Secretary Michael Gove recently announced a new education league table for England, showing which state schools are preparing children to be "university-ready" — numbers of children going on to graduate with an honours degree. (Presumably everyone from a private school graduates with honours.)
Why not go further and shrink-wrap kids, slap on an "oven-ready" — oops, "university-ready" — label and ship them off? Any rejected as "non-university-ready" could be ground down and turned into "worker nuggets".
In the 20-odd years since the introduction of England's national curriculum (not the United Kingdom — no grudges against the Scots, Welsh or Northern Irish, please) the pressures on schools, parents and, particularly, children, have been worse than anyone predicted. As Australia gets set to have its own national curriculum, what might be learnt from England's follies?
A national curriculum on its own may be no bad thing. The rot sets in with the paraphernalia for measuring results and "standards". National testing is not evil but when the results were used to put England's schools into league tables, the mischief started. At middle-class dinner tables from London to Manchester, parents anxiously discuss whether they sent their children to the "right" school, or plot the "best" catchment area to move to. Parents without the savvy, mobility, or SUV to get the kids to school, are left with little choice and often with schools that go into a tailspin as their results drop.
Will data from My School become more public and a similar tiering of the education system develop in Australia?
Now, yet another review of England's national curriculum (new government, new curriculum) came with Mr Gove announcing that England had "sunk in international league tables and the national curriculum is substandard". One review panel expert declared the national curriculum "on the front line of the battle for the UK's future competitiveness". Ah, the Cold War may be a distant memory but England still has a battle to fight.
The saddest aspect in all the talk of "university-ready" children and global competition is the scant sense that education might provide a good experience for children and adolescents in the here and now. Everything is about getting them ready for the next stage — what the universities need, what the global economies want. Just like the youngsters in Never Let Me Go. What happened to thinking about what a six-year-old needs to be a six-year-old?
Of course Australia is more moderate, although the opening of the Melbourne Declaration on Educational Goals for Young Australians does state: "In the 21st century Australia's capacity to provide a high quality of life for all will depend on the ability to compete in the global economy on knowledge and innovation."
There is another way. As British academic Robin Alexander puts it, global perspectives are often "contra-national" rather than inter-national. Continuing to see the world in terms of trade and a need for local, national, economic supremacy may no longer be viable or sustainable. Rather than educating children to be global competitors, we would be better off helping them see themselves as global citizens, in the broadest sense of the moral obligation that carries.
Everyone can gain from a global education based on co-operation and collectivity rather than competition and supremacy. An education based on acknowledging that globally we are more interdependent than independent. An education working to help the world be united, not divided. That would be an education system to be proud of globally.
blog comments powered by Disqus
A curve stitch in time

I wish I hadn’t read the Harry Potter books.
Then I’d be able to enjoy them again for the first time.
I sympathised with this girl’s comment, overheard on the train home from work. We could all list a multitude of experiences that thrilled and engaged the first time round but lost frisson with repetition. Of course we can’t go back (and if we could return to the first time then we wouldn’t be getting the excitement twice over anyway), but one of the joys of teaching is to witness children’s ‘Aah’ or ‘Aha’ moments - a vicarious re-living of experiences.
Her comment got me mulling over what mathematics I could remember learning that, first time round, had caught my interest. I couldn’t recall much of my primary maths lessons other than doing pages of ‘sums’ and I enjoyed those more for the precision of neatly penning one-digit-to-one-square than for the pleasure of the calculations themselves. Nice graphics, dull mathematics.
Then I recalled a student teacher introducing us to curve stitching. No longer fashionable, so for anyone not familiar with the idea, it involves constructing two perpendicular axes with scales from, say 1 to 9, and then joining up the pairs of points on the axes that total to ten. I remembered forcing a bodkin threaded with thick yellow wool through fibrous unbleached board. As more pairs got joined a little bit of mathematical magic happened: the straight lines combined to reveal a curve.
Curve stitching probably isn’t taught much now as it lacks immediate application and doesn’t appear on international tests. A shame since I think it pinned down some important impressions for me. First, it introduced me to the world of mathematics beyond arithmetic and showed me the beauty in that world. Second, when, years later, I met calculus and differentiation, the traces in my body from, literally, stitching a curve out of straight lines, gave me the physical grounding of the meaning of tangents to curves.
I can’t remember the name of the student teacher and I doubt she chose to teach curve stitching as a foundation for calculus. But we should not underestimate how what we teach today may echo down the years. Another joy of teaching.
blog comments powered by Disqus
Zen and the art of arithmetic
When

Kenneth R Beittel, Zen and the Art of Pottery
Over the holidays I took a pottery course. Our teacher, Jane Sawyer, trained in Japan and introduced us to some classical techniques, beginning with 'wedging' the clay: a strenuous kneading that in her hands produced a beautiful nautilus spiral, but in my hands turned to, well, a knarled lump of clay. But I got a feel for the clay as I rolled and squished and stretched it.
At the potter's wheel, trying to 'centre' my clay I was struck by the centuries of tradition behind replacing the hand with the bowl and got to thinking about tradition in teaching mathematics. Perhaps the 'traditional' algorithms for addition, subtraction, long multiplication and long division are the mathematical equivalent of throwing a pot and teaching these means celebrating our mathematical heritage, joining the long line of those before us who had gone through similar processes.
After lunch, two things made me rethink this reverie. First was when Jane showed slides of Japanese pots, including one of an exquisitely elaborate pot more than 4000 years old. Mathematical algorithms, in that time scale, seem rather less 'traditional' having only been around a few hundred years.
Second Jane mentioned that the hard labour of wedging clay isn't so important now as many potters happily use a machine to do this (which has also opened it up to more women potters). I decided that algorithms are more like wedging than throwing. We have machines that can wedge our calculations, machines that can free us up for the creative part of mathematics: solving problems. We might want children to experience algorithms, to know of their place in the mathematics tradition, but they are not the core of the discipline. And children certainly do not need to spend hours being drilled in them.
As my first wobbly but complete bowl came off the wheel, I felt the same satisfaction that I get from resolving a mathematical problem after several false starts. That's the tradition of mathematics we must pass on.
