Mindful mathematics
04/06/11 10:05 Filed in: Mindful learning
Ellen Langer
I was lucky this week to hear the wondrous Ellen Langer give a talk. If you haven’t come across it, then I highly recommend her book ‘The Power of Mindful learning’. She spoke for over two hours and it was pure enchantment.
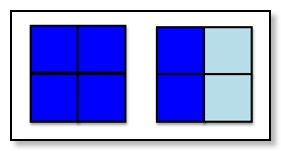
One of the key findings from Prof Langer’s research of over 30 years is that learning is more powerful if we are mindful of the conditionality of most ‘facts’. For example, in a lesson on fractions, a diagram like the one above is usually introduced as the pale blue shows ½. In contrast, Langer argues that presenting the diagram as it ‘could’ represent ½ makes the learning mindful and deeper.
Part of the argument for this is that the ‘fractions’ are not in the diagram itself but they are the result of someone somewhere at sometime deciding how the diagram should be read. In other words, there was a choice to be made over what mathematics the diagram could represent - not what it does represent.
By re-introducing this choice and conditionality into the teaching of it, the learner is encouraged not simply to take the mathematics for granted, nor to just commit something to memory. In contrast they engage in mathematical thinking.
So what else could the pale blue represent?
Well, it could be different if we are mindful of not taking for granted the condition that the ‘unit’ has to be four small squares. Under the condition of the whole picture as the unit, then the pale blue could be ¼.
Or we could set up the condition of comparing the pale blue to the dark blue and so the pale blue could be ⅓. The possibilities do not end there.
Of course this does not mean telling children that ‘anything goes’ and they are free to choose any reading they like. But by implicitly acknowledging in our teaching the human agency in mathematics we could help more learners come to see mathematics as a human endeavour worth engaging with, rather than something to keep at arm’s length.
blog comments powered by Disqus
blog comments powered by Disqus
